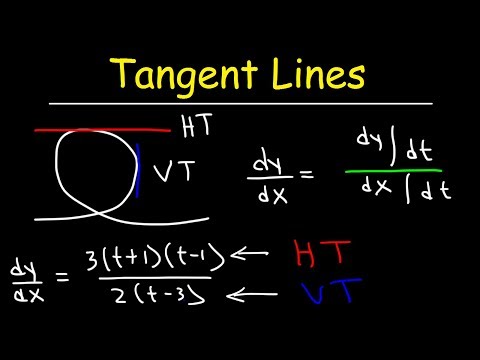
Garis tangen mendatar adalah ciri matematik pada graf, yang terletak di mana fungsi derivatif adalah sifar. Ini kerana, dengan definisi, derivatif memberikan cerun garis tangen. Garis mendatar mempunyai cerun sifar. Oleh itu, apabila derivatif adalah sifar, garis tangen adalah mendatar. Untuk mencari garis tangen mendatar, gunakan derivatif fungsi untuk mencari nol dan pasangkannya kembali ke persamaan asal. Garis tangen mendatar adalah penting dalam kalkulus kerana ia menunjukkan titik maksimum atau minimum tempatan dalam fungsi asal.
Ambil derivatif fungsi tersebut. Bergantung kepada fungsi tersebut, anda boleh menggunakan peraturan rantai, peraturan produk, peraturan quotient atau kaedah lain. Sebagai contoh, diberikan y = x ^ 3 - 9x, mengambil derivatif untuk mendapatkan y = 3x ^ 2 - 9 menggunakan peraturan kuasa yang menyatakan mengambil derivatif x ^ n, akan memberi anda n * x ^ (n-1) .
Faktor derivatif untuk membuat mencari sifar lebih mudah. Terus dengan contoh, y = 3x ^ 2 - 9 faktor kepada 3 (x + sqrt (3)) (x-sqrt (3))
Tetapkan derivatif sama dengan sifar dan selesaikan "x" atau pembolehubah bebas dalam persamaan. Dalam contoh, menetapkan 3 (x + sqrt (3)) (x-sqrt (3)) = 0 memberikan x = -sqrt (3) dan x = sqrt (3) dari faktor kedua dan ketiga. Faktor pertama, 3, tidak memberi kita nilai. Nilai-nilai ini adalah nilai "x" dalam fungsi asal yang sama ada titik maksimum atau minimum.
Palamkan nilai yang diperoleh pada langkah sebelumnya kembali ke fungsi asal. Ini akan memberi anda y = c untuk beberapa "c" malar. Ini adalah persamaan garis tangen mendatar. Plug x = -sqrt (3) dan x = sqrt (3) kembali ke fungsi y = x ^ 3 - 9x untuk mendapatkan y = 10.3923 dan y = -10.3923. Ini adalah persamaan garis tangen melintang untuk y = x ^ 3 - 9x.