Kandungan
Anda boleh mengira daya dan tindakan sistem takal melalui penerapan undang-undang Newtons.Undang-undang kedua berfungsi dengan kekuatan dan percepatan; Undang-undang ketiga menunjukkan arah kuasa dan bagaimana daya ketegangan mengimbangi daya graviti.
Pulleys: The Ups and Downs
Kren adalah roda berputar yang dipasang dengan rim cembung melengkung dengan tali, tali pinggang atau rantai yang boleh bergerak di sepanjang rim roda untuk mengubah arah daya tarikan. Ia mengubah atau mengurangkan usaha yang diperlukan untuk menggerakkan objek berat seperti enjin kereta dan lif. Sistem pulley asas mempunyai objek yang disambungkan ke satu hujung manakala daya mengawal, seperti dari otot orang atau motor, menarik dari hujung yang lain. Sistem pulley Atwood mempunyai kedua-dua hujung tali pulley disambungkan kepada objek. Jika kedua-dua objek mempunyai berat yang sama, kren tidak akan bergerak; Walau bagaimanapun, tarikan kecil di kedua-dua belah pihak akan memindahkannya ke satu arah atau yang lain. Sekiranya beban adalah berbeza, berat yang lebih berat akan mempercepatkan sementara beban yang lebih ringan mempercepatkan.
Sistem Pulley Asas
Newton undang-undang kedua, F (daya) = M (jisim) x A (pecutan) menganggap pulley tidak mempunyai geseran dan anda mengabaikan jisim pulleys. Newtons undang-undang ketiga mengatakan bahawa untuk setiap tindakan terdapat tindak balas yang sama dan bertentangan, maka jumlah kekuatan sistem F akan sama dengan kekuatan dalam tali atau T (tegangan) + G (daya graviti) yang menarik pada beban. Dalam sistem pulley asas, jika anda menggunakan kekuatan lebih besar daripada massa, jisim anda akan mempercepatkan, menyebabkan F menjadi negatif. Jika massa mempercepatkan, F adalah positif.
Kirakan ketegangan dalam tali menggunakan persamaan berikut: T = M x A. Empat contoh, jika anda cuba mencari T dalam sistem takal asas dengan jisim terpasang 9g mempercepat ke atas pada 2m / s² maka T = 9g x 2m / s² = 18gm / s² atau 18N (newtons).
Kirakan daya yang disebabkan oleh graviti pada sistem pulley asas menggunakan persamaan berikut: G = M x n (pecutan graviti). Percepatan graviti adalah tetap sama dengan 9.8 m / s². Jisim M = 9g, jadi G = 9g x 9.8 m / s² = 88.2gm / s², atau 88.2 newtons.
Masukkan daya ketegangan dan daya graviti yang baru saja dikira ke persamaan asal: -F = T + G = 18N + 88.2N = 106.2N. Kekuatannya adalah negatif kerana objek dalam sistem pulley mempercepatkan ke atas. Negatif dari daya dipindahkan ke penyelesaian jadi F = -106.2N.
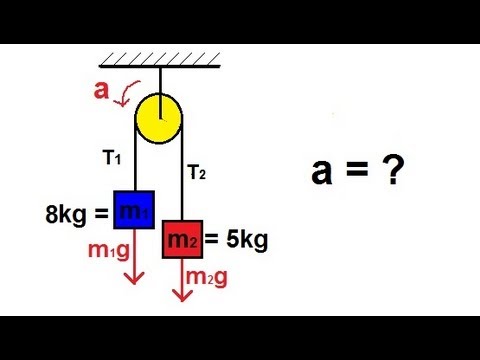
Atwood Pulley System
Persamaan, F (1) = T (1) - G (1) dan F (2) = -T (2) + G (2), mengandaikan pulley tidak mempunyai geseran atau massa. Ia juga menganggap jisim dua adalah lebih besar daripada jisim. Jika tidak, saksikan persamaan.
Kirakan ketegangan pada kedua-dua belah sistem pulley menggunakan kalkulator untuk menyelesaikan persamaan berikut: T (1) = M (1) x A (1) dan T (2) = M (2) x A (2). Sebagai contoh, jisim objek pertama sama dengan 3g, jisim objek kedua sama dengan 6g dan kedua-dua belah tali mempunyai pecutan yang sama bersamaan dengan 6.6m / s². Dalam kes ini, T (1) = 3g x 6.6m / s² = 19.8N dan T (2) = 6g x 6.6m / s² = 39.6N.
Kirakan daya yang disebabkan oleh graviti pada sistem pulley asas menggunakan persamaan berikut: G (1) = M (1) x n dan G (2) = M (2) x n. Percepatan graviti n adalah tetap sama dengan 9.8 m / s². Jika jisim pertama M (1) = 3g dan jisim kedua M (2) = 6g, maka G (1) = 3g x 9.8 m / s² = 29.4N dan G (2) = 6g x 9.8 m / s² = 58.8 N.
Masukkan ketegangan dan daya graviti sebelum ini dikira untuk kedua-dua objek ke dalam persamaan asal. Untuk objek pertama F (1) = T (1) - G (1) = 19.8N - 29.4N = -9.6N, dan bagi objek kedua F (2) = -T (2) + G (2) -39.6N + 58.8N = 19.2N. Hakikat bahawa daya objek kedua lebih besar daripada objek pertama dan bahawa daya objek pertama menunjukkan negatif bahawa objek pertama mempercepat ke atas sementara objek kedua bergerak ke bawah.