
Autocorrelation adalah kaedah statistik yang digunakan untuk analisis siri masa. Tujuannya adalah untuk mengukur korelasi dua nilai dalam set data yang sama pada langkah masa yang berbeza. Walaupun data masa tidak digunakan untuk mengira autokorelasi, kenaikan masa anda harus sama untuk mendapatkan hasil yang bermakna. Pekali autokorelasi berfungsi dua tujuan. Ia boleh mengesan tidak rawak dalam set data. Jika nilai dalam set data tidak rawak, maka autokorelasi dapat membantu penganalisis memilih model siri masa yang sesuai.
Kirakan min, atau purata, untuk data yang anda sedang analisa. Maksudnya ialah jumlah semua nilai data dibahagikan dengan bilangan nilai data (n).
Tentukan lag masa (k) untuk pengiraan anda. Nilai lag ialah integer yang menunjukkan berapa banyak langkah yang memisahkan satu nilai dari yang lain. Sebagai contoh, ketinggian antara (y1, t1) dan (y6, t6) adalah lima, kerana terdapat 6 - 1 = 5 langkah masa antara kedua nilai tersebut. Apabila ujian untuk rawak, anda biasanya akan mengira satu pekali autokorelasi menggunakan lag k = 1, walaupun nilai lag lain juga akan berfungsi. Apabila anda menentukan model siri masa yang sesuai, anda perlu mengira siri nilai autokorelasi, menggunakan nilai lag yang berbeza untuk setiap satu.
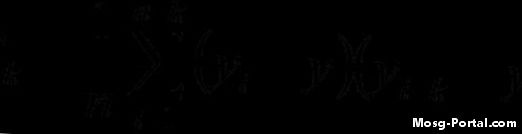
Kirakan fungsi autokovarians menggunakan formula yang diberikan. Sebagai contoh, adakah anda mengira lelaran ketiga (i = 3) menggunakan lag k = 7, maka pengiraan untuk lelaran itu akan kelihatan seperti ini: (y3 - y-bar) (y10 - y-bar) nilai "i" dan kemudian ambil jumlah dan bahagikannya dengan bilangan nilai dalam set data.
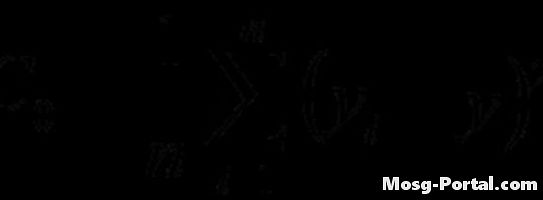
Kirakan fungsi varians menggunakan formula yang diberikan. Pengiraan adalah sama dengan fungsi autokovarian, tetapi lag tidak digunakan.

Bahagikan fungsi autokovarians dengan fungsi varians untuk mendapatkan pekali autokorelasi. Anda boleh melangkau langkah ini dengan membahagikan formula untuk kedua-dua fungsi seperti yang ditunjukkan, tetapi banyak kali, anda memerlukan autokovarian dan varians untuk tujuan lain, jadi praktikal untuk mengira mereka secara individu juga.