Kandungan
- Dasar-dasar Gerakan
- Persamaan Gelombang Angular
- Persamaan Gerakan Putaran
- Kuantiti dan Ekspresi yang berkaitan
- Gelombang Angular vs. Velocity Linear
Dalam wacana sehari-hari, "kelajuan" dan "halaju" sering digunakan secara bergantian. Namun dalam fizik, istilah-istilah ini mempunyai makna tertentu dan berbeza. "Kelajuan" ialah kadar pergeseran sesuatu objek di ruang angkasa, dan ia hanya diberikan oleh nombor dengan unit tertentu (selalunya dalam meter per saat atau batu sejam). Sebaliknya, halaju adalah kelajuan ditambah dengan arah. Kelajuan, kemudian, dipanggil kuantiti skalar, manakala halaju adalah kuantiti vektor.
Apabila sebuah kereta sedang mengepung sepanjang lebuh raya atau baseball mengepung melalui udara, kelajuan objek tersebut diukur dengan merujuk kepada tanah, sedangkan halaju itu memasukkan lebih banyak maklumat. Contohnya, jika anda dalam kereta yang bergerak sejauh 70 batu sejam di Interstate 95 di Pantai Timur Amerika Syarikat, ia juga berguna untuk mengetahui sama ada ia menuju ke arah timur laut ke arah Boston atau ke arah selatan ke arah Florida. Dengan besbol, anda mungkin ingin tahu jika koordinat y berubah dengan lebih cepat daripada koordinat x (bola terbang) atau jika sebaliknya adalah benar (pemacu garis). Tetapi bagaimana pula dengan putaran tayar atau putaran (putaran) besbol ketika kereta dan bola bergerak menuju destinasi utama mereka? Untuk jenis soalan ini, fizik menawarkan konsep halaju sudut.
Dasar-dasar Gerakan
Perkara bergerak melalui ruang fizikal tiga dimensi dalam dua cara utama: terjemahan dan putaran. Terjemahan adalah anjakan seluruh objek dari satu lokasi ke tempat lain, seperti kereta memandu dari New York City ke Los Angeles. Sebaliknya, putaran adalah gerakan kitaran sesuatu objek di sekitar titik tetap. Banyak objek, seperti besbol dalam contoh di atas, menunjukkan kedua-dua jenis pergerakan pada masa yang sama; sebagai bola terbang bergerak melalui udara dari plat rumah ke arah pagar luar, ia juga berputar pada kadar tertentu di sekitar pusatnya sendiri.
Menggambarkan dua jenis gerakan ini dianggap sebagai masalah fizik yang berasingan; iaitu ketika menghitung jarak bola bergerak melalui udara berdasarkan hal-hal seperti sudut peluncuran awal dan kelajuan yang mana ia meninggalkan kelelawar, anda boleh mengabaikan putarannya, dan apabila mengira putarannya, anda boleh memperlakukannya sebagai duduk dalam satu tempat untuk tujuan sekarang.
Persamaan Gelombang Angular
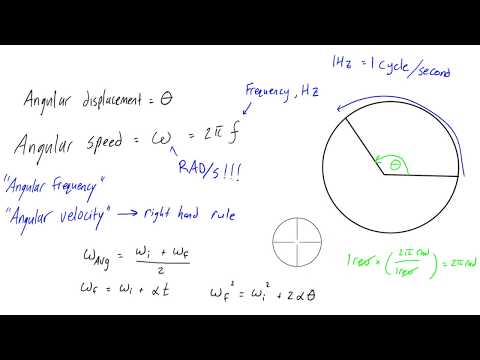
Pertama, apabila anda bercakap tentang apa-apa "sudut", sama ada halaju atau beberapa kuantiti fizikal lain, sedar bahawa, kerana anda berhadapan dengan sudut, anda bercakap mengenai perjalanan dalam kalangan atau sebahagian daripadanya. Anda mungkin ingat dari geometri atau trigonometri bahawa lilitan bulatan adalah masa diameternya pi yang tetap, atau πd. (Nilai pi kira-kira 3.14159.) Ini lebih umum dinyatakan dari segi radius bulatan r, iaitu separuh diameter, menjadikan lilitan itu 2πr.
Di samping itu, anda mungkin belajar di mana-mana sepanjang bulatan terdiri daripada 360 darjah (360 °). Jika anda bergerak jarak S sepanjang bulatan, daripada anjakan sudut θ adalah sama dengan S / r. Satu revolusi penuh, kemudian, memberikan 2πr / r, yang hanya meninggalkan 2π. Ini bermakna sudut kurang bahawa 360 ° boleh dinyatakan dalam bentuk pi, atau dengan kata lain, seperti radian.
Mengambil semua maklumat ini bersama-sama, anda boleh menyatakan sudut, atau bahagian bulatan, dalam unit selain darjah:
360 ° = (2π) radian, atau
1 radian = (360 ° / 2π) = 57.3 °,
Sedangkan halaju linear dinyatakan dalam panjang per unit waktu, halaju sudut diukur dalam radian per unit waktu, biasanya per detik.
Sekiranya anda tahu bahawa zarah bergerak dalam laluan bulat dengan halaju v pada jarak jauh r dari pusat bulatan, dengan arah v sentiasa berserenjang dengan jejari bulatan, maka halaju sudut boleh ditulis
ω = v / r,
di mana ω adalah huruf Greek omega. Unit halaju sudut adalah radians sesaat; anda juga boleh merawat unit ini sebagai "detik balas," kerana hasil v / r m / s dibahagikan dengan m, atau s-1, bermakna bahawa radians adalah secara teknikalnya adalah kuantiti tanpa unit.
Persamaan Gerakan Putaran
Formula pecutan sudut diperolehi dengan cara yang sama penting seperti formula halaju sudut: Ini adalah hanya pecutan linear dalam arah yang berserenjang dengan jejari bulatan (secara bersamaan, pecutan di sepanjang tangen ke laluan bulat pada mana-mana titik) dibahagikan dengan jejari bulatan atau bahagian bulatan, iaitu:
α = at/ r
Ini juga diberikan oleh:
α = ω / t
kerana untuk gerakan bulat, at = ωr / t = v / t.
α, seperti yang anda ketahui, adalah huruf Greek "alpha." The subscript "t" di sini menandakan "tangen."
Walau bagaimanapun, dengan pantas, gerak putaran mempunyai pecutan yang lain, yang dipanggil centripetal ("mencari pusat") pecutan. Ini diberikan oleh ungkapan:
ac = v2/ r
Percepatan ini diarahkan ke titik di mana objek yang bersangkutan berputar. Ini mungkin kelihatan aneh, kerana objek tidak lagi dekat dengan titik pusat ini sejak radius r telah ditetapkan. Fikirkan pecutan centripetal sebagai jatuh bebas di mana tidak ada bahaya objek yang memukul tanah, kerana daya yang menggambar objek ke arahnya (biasanya graviti) betul-betul diimbangi oleh pecutan tangen (linear) yang digambarkan oleh persamaan pertama dalam bahagian ini. Jika ac tidak sama dengan at, objek itu akan terbang ke ruang angkasa atau tidak lama lagi akan jatuh ke tengah-tengah bulatan.
Kuantiti dan Ekspresi yang berkaitan
Walaupun halaju sudut biasanya dinyatakan, seperti yang dinyatakan, dalam radians sesaat, mungkin ada contoh di mana ia lebih baik atau perlu menggunakan darjah sesaat sebaliknya, atau sebaliknya, untuk menukar dari darjah ke radian sebelum menyelesaikan masalah.
Katakan anda diberitahu bahawa sumber cahaya berputar melalui 90 ° setiap saat pada halaju yang tetap. Apakah halaju sudutnya dalam radian?
Pertama, ingati bahawa radians 2π = 360 °, dan menetapkan bahagian:
360 / 2π = 90 / x
360x = 180π
x = ω = π / 2
Jawapannya adalah satu setengah radian pi per saat.
Sekiranya anda dimaklumkan lagi bahawa pancaran cahaya mempunyai jarak 10 meter, apa yang akan menjadi hujung rasuk linear halaju v, pecutan sudutnya α dan pecutan centripetalnya ac?
Untuk menyelesaikannya v, dari atas, v = ωr, di mana ω = π / 2 dan r = 10m:
(π / 2) (10) = 5π rad / s = 15.7 m / s
Untuk menyelesaikannya α, tambahkan satu unit masa lagi kepada penyebut:
α = 5π rad / s2
(Perhatikan bahawa ini hanya berfungsi untuk masalah di mana halaju sudut adalah malar.)
Akhirnya, juga dari atas, ac = v2/ r = (15.7)2/ 10 = 24.65 m / s2.
Gelombang Angular vs. Velocity Linear
Membangunkan pada masalah sebelumnya, bayangkan diri anda dalam satu rombongan yang sangat besar, satu dengan jejari yang tidak mungkin 10 kilometer (10,000 meter). Pusingan riang ini menjadikan satu revolusi lengkap setiap 1 minit dan 40 saat, atau setiap 100 saat.
Satu akibat dari perbezaan antara halaju sudut, yang bebas daripada jarak dari paksi putaran, dan halaju pekeliling linear, yang tidak, adalah bahawa dua orang mengalami sama ω mungkin mengalami pengalaman fizikal yang jauh berbeza. Sekiranya anda berada sejauh 1 meter dari pusat ini jika halaju putative, berani anda, halaju linear (tangential) anda ialah:
ωr = (2π rad / 100 s) (1 m) = 0.0628 m / s, atau 6.29 cm (kurang daripada 3 inci) sesaat.
Tetapi jika anda berada di tepi raksasa ini, halaju linear anda ialah:
ωr = (2π rad / 100 s) (10,000 m) = 628 m / s. Thats kira-kira 1,406 batu sejam, lebih cepat daripada peluru. Bertahan!